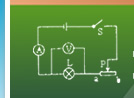
实验目的

　　学习用单摆测定重力加速度的方法，测出当地的重力加速度。

实验仪器

　　摆球，秒表，铁架台，铁夹，米尺或钢卷尺，游标卡尺，细线等。

实验原理

　　单摆在摆角很小的情况下，可以看作简谐振动，其固有周期公式为由此得：  。据此，通过实验方法测出摆长l和周期T，即可计算出当地的重力加速度。

实验步骤

　　1、将细线穿过金属小球上的小孔，在细线的一端打一个稍大一点的结，制成一个单摆。
　　2、将铁架固定在铁架台上端，铁架台放在桌边，使铁架伸出桌面，然后把单摆固定在铁夹上，使摆球自由下垂。
　　3、用刻度尺量出摆长（摆求静止时悬点到摆球球心的距离）。
　　4、把摆球从平衡位置拉开一个角度，然后无初速释放小球。当摆球摆动稳定以后经过最低点时用秒表开始计时，测出单摆30～50次全振动的时间，求出一次振动时间及单摆的周期。
　　5、反复测量三次，计算出周期的平均值，然后利用公式计算出重力加速度。

注意事项

　　1、摆线要用细而不易伸长的线，悬点要固定不变，不能把摆线随意缠绕在铁夹上，以免悬点松动，引起摆长变化．悬挂单摆时可用铁夹把细线上端夹紧，也可用烧瓶夹夹紧两块小木板，以此夹紧摆线。
　　2、摆长以1m左右为宜，摆长是指从悬点到球心的距离，测摆长应在单摆竖直悬挂的状态下进行。如果只用一把米尺测量摆长，可以让米尺与悬线平行，尺上端的零刻度线与过悬点的水平线重合，尺下端与小球相切，切点处的读数就是摆长。或者用米尺测出摆线的长度、用游标卡尺或两把三角尺测出小球直径，则摆线长加小球半径就是摆长。
　　3、注意摆动时摆角不能过大。
　　4、要让单摆在竖直平面内摆动，不要形成锥摆，测定单摆振动周期时，可事前在平衡位置正下方放一支铅笔或一块橡皮作为记号，在摆球经过平衡位置时开始默数，默数全振动次数要与振动周期同步，注意摆球每经过平衡位置两次才完成一次全振动。开头用倒数的方法、后来才顺数：即默数“5，4，3，2，1，0，1，2，…30”，数到“0”时启动秒表，数至30”时关闭秒表。
 

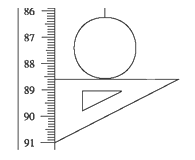
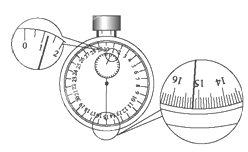
　　1、在做“用单摆测定重力加速度”的实验时，用摆长L和周期T计算重力加速度的公式是g=_____。如果已知摆球直径为2.00cm，让刻度尺的零点对准摆线的悬点，摆线竖直下垂，如图示，那么单摆摆长是_____。如果测定了40次全振动的时间如图中秒表所示，那么秒表读数是_____s。单摆的摆动周期是_____s。

　　2、某同学想在家里做用单摆测定重力加速度的实验，但没有合适的摆球，他找到了一块大小为3cm左右，外形不规则的大理石块代替小球。他设计的实验步骤是：

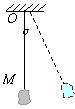
　　A. 将石块用细尼龙线系好，结点为M，将尼龙线的上端固定于O点
  　 B. 用刻度尺测量OM间尼龙线的长度L作为摆长
  　 C. 将石块拉开一个大约α=30°的角度，然后由静止释放
  　 D. 从摆球摆到最高点时开始计时，测出30次全振动的总时间t，，由T=t/30得出周期
 　   E. 改变OM间尼龙线的长度再做几次实验，记下相应的L和T
 　   F.求出多次实验中测得的平均值作为计算时使用的数据，代入公式 求出重力加速度g
 　  ⑴你认为该同学以上实验步骤中有重大错误的是_______________。为什么?
 　  ⑵该同学用OM的长作为摆长，这样做引起的系统误差将使重力加速度的测量值比真实值偏大还是偏小?________。
　 （3）你认为用什么方法可以解决摆长无法准确测量的困难?

      3、某同学在用单摆测定重力加速度的实验中，测量5种不同摆长情况下单摆的振动周期，记录表格如下：

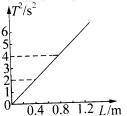
关于重力加速度

　　重力加速度g值的准确测定对于计量学、精密物理计量、地球物理学、地震预报、重力探矿和空间科学等都具有重要意义。
　　最早测定重力加速度的是伽利略。约在1590年，他利用倾角为θ的斜面将g的测定改为测定微小加速度a=gsinθ。1784年，G•阿特武德将质量同为M的重物用绳连接后，挂在光滑的轻质滑轮上，再在另一个重物上附加一重量小得多的重物m，使其产生一微小加速度a＝mg/（2M＋m），测得a后，即可算出g。
　　1888年，法国军事测绘局使用新的方法进行了g值的计量.它的原理简述为：若一个物体如单摆那样以相同的周期绕两个中心摆动，则两个中心之间的距离等于与上述周期相同的单摆的长度。当时的计量结果为：g=9.80991m/s²。
　　1906年，德国的库能和福脱万勒用相同的方法在波茨坦作了g值的计量，作为国际重力网的参考点，即称为“波茨坦重力系统”的起点，其结果为g（波茨坦）=9.81274m/s²。
　　根据波茨坦得到的g值可以通过相对重力仪来求得其他地点与它的差值，从而得出地球上各地的g值，这样建立起来的一系列g值就称为波茨坦重力系统。国际计量局在1968年10月的会议上推荐，自1969年1月1日起，g（波茨坦）减小到9.81260m/s²。根据上述修正了的波茨坦系统，在地球上的一级点位置的g值的不确定度可小于5×10^-7。